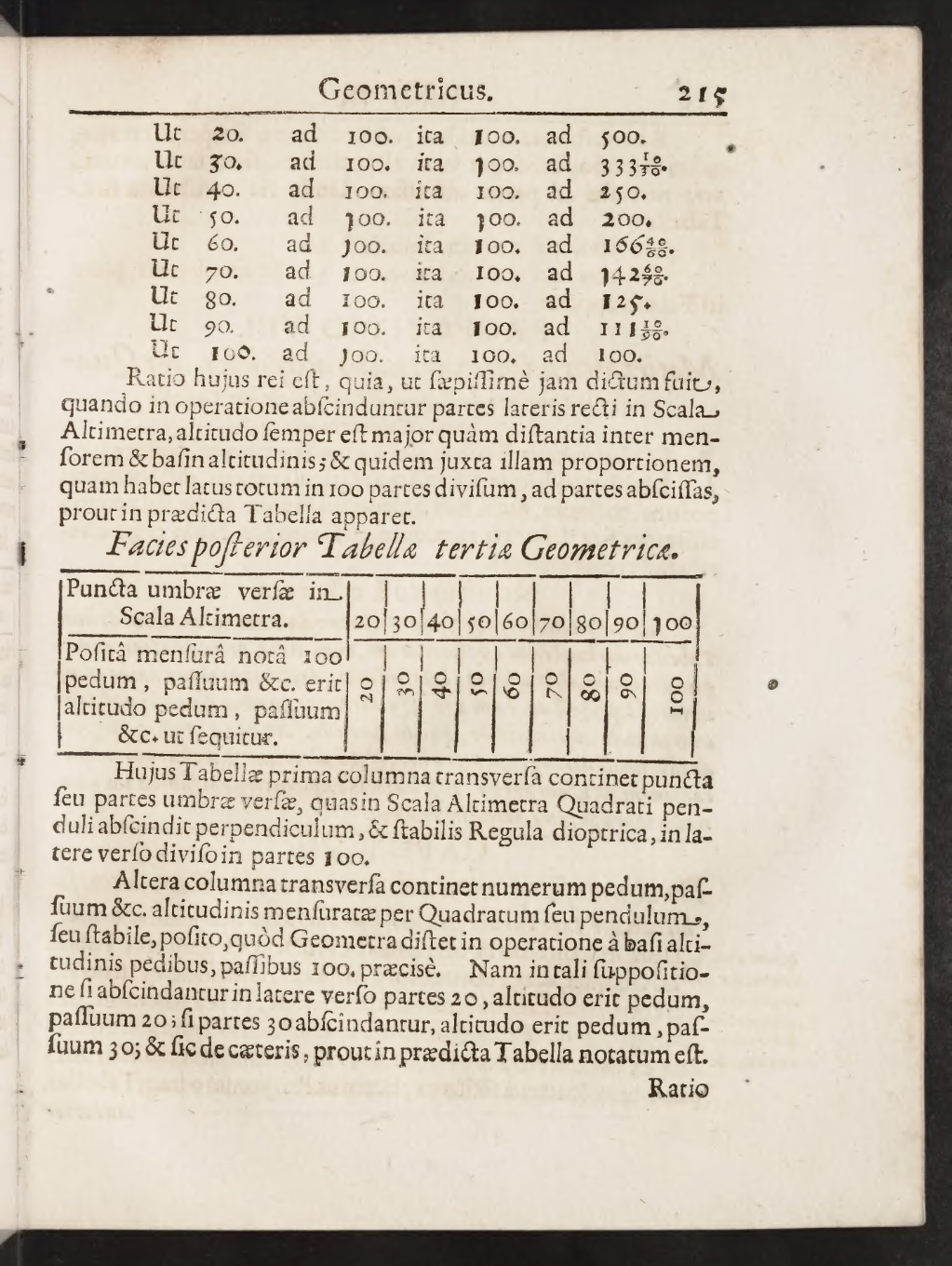
| Ut | 20 | ad | 100 | ita | 100 | ad | 500 |
| Ut | 30 | ad | 100 | ita | 100 | ad | 333 10/30 |
| Ut | 40 | ad | 100 | ita | 100 | ad | 250 |
| Ut | 50 | ad | 100 | ita | 100 | ad | 200 |
| Ut | 60 | ad | 100 | ita | 100 | ad | 166 40/60 |
| Ut | 70 | ad | 100 | ita | 100 | ad | 142 60/70 |
| Ut | 80 | ad | 100 | ita | 100 | ad | 125 |
| Ut | 90 | ad | 100 | ita | 100 | ad | 111 10/90 |
| Ut | 100 | ad | 100 | ita | 100 | ad | 100 |
Ratio hujus rei est, quia, ut saepissime iam dictum fuit,
quando in operatione abscinduntur partes lateris recti in Scala
Altimetra, altitudo semper est maior quam distantia inter mensorem
& basin altitudinis; & quidem iuxta illam proportionem,
quam habet latus totum in 100 partes divisum, ad partes abscissas,
prout in praedicta Tabella apparet.
| Puncta umbrae versae in Scala Altimetra | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| Posita mensuram notam 100 pedum, passuum &c. erit altitudo pedum, passuum &c. ut sequitur | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
Huius Tabellae prima columna transversa continet puncta
seu partes umbrae versae, quas in Scala Altimetra Quadrati penduli
abscindit perpendiculum, & stabils Regula dioptrica, in latere
verso diviso in partes 100.
Altera columna transversa continet numerum pedum, passuum
&c. altitudinis mensurare per Quadratum seu pendulum,
seu stabile, positio, quod Geometra distet in operatione a basi altitudinis
pedibus, passibus 100, praecise. Nam in tali suppositione
si abscindantur in latere verso partes 20, altitudo erit pedum,
passuum 20; si partes 30 abscindantur, altitudo erit pedum, passuum
30; & sic de caeteris, prout in praedicta Tabella notarum est.